What is maximum flow problem?
The maximum flow problem is a problem for calculation
the maximum amount of material that can flow from source to sink. The material
flowing through these networks can be anything like water flowing through
pipes, driving traffic through a city, etc. This maximum flow problem could be
solved through two major algorithms, Ford-Fulkerson algorithm and Dinic’s
Algorithm. Here we will discuss Ford-Fulkerson Algorithm.
Ford-Fulkerson Algorithm
Ford-Fulkerson Algorithm is a greedy approach used for
calculation of maximum flow in a graph or a given network. Before starting one
must know some basic terminologies used while calculation.
Source(s): The source is a starting vertex which has
all the outward edge and not a single inward edge.
Sink(t): Sink is the end point of the path which
contains all inward edges.
Bottleneck Capacity: It is the minimum capacity of any
edge of the chosen path.
Residual Capacity: It is original capacity minus the
current flow.
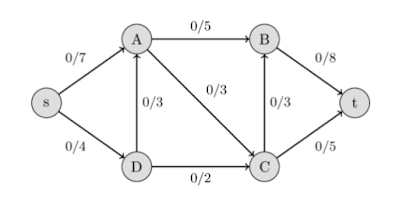
Let’s understand it with an example:
Initially start with a flow of 0. The left part is
denoted as flow and the right part is capacity of that edge.
1) Now,
we can take the augmented path as s –
A – B – t with residual capacity as 7,5
and 8. Now the bottleneck capacity is for this path is 5 as it is minimum. Now
flow becomes 5.
Once the residual capacity for a specific edge becomes
zero i.e., original capacity minus current flow is zero then that edge gets
blocked. We can’t consider that edge for finding further augmented path.
2) Now
we look for another augmented path i.e. s
– D – A – C – t with residual
capacities as 4, 3, 3 and 5. The bottleneck capacity is 3 therefore, flow
becomes 5 + 3 = 8.
3) We
take s – D – C – B – t as our next
augmented path with residual capacities as 1, 2, 3 and 3. The bottleneck
capacity is 1 therefore, flow becomes 5 + 3 + 1 = 9.
So, now there is no augmented path left between s to
t. Therefore, the maximum possible flow is 9.
Time Complexity
Time complexity of the above algorithm is O(maxflow *
E). We run a loop while there is an augmenting path. In worst case, we may add
1 unit flow in every iteration. Therefore, the time complexity becomes
O(maxflow * E).
Applications
Water distribution pipeline network
Traffic driving through a city
Sensor placement for homeland security
Network connectivity
References
1. http://www.ijsrp.org/research-paper-1218/ijsrp-p8441.pdf
2. https://en.wikipedia.org/wiki/Ford%E2%80%93Fulkerson_algorithm
3. https://www.youtube.com/watch?v=NwenwITjMys
4. https://downey.io/blog/max-flow-ford-fulkerson-algorithm-explanation/






Comments